1110. Delete Nodes And Return Forest

Problem

Question

Given the root of a binary tree, each node in the tree has a distinct value.

After deleting all nodes with a value in to_delete, we are left with a forest (a disjoint union of trees).

Return the roots of the trees in the remaining forest. You may return the result in any order.

Example 1:

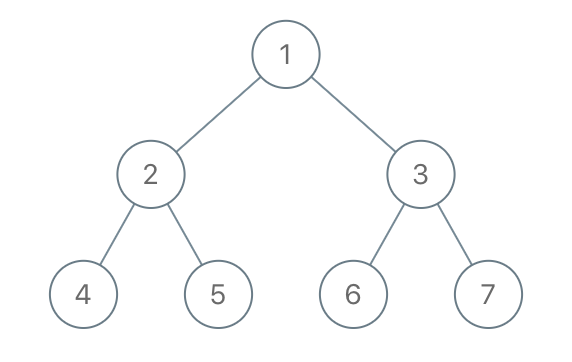
Input: root = [1,2,3,4,5,6,7], to_delete = [3,5] Output: [[1,2,null,4],[6],[7]]

Example 2:

Input: root = [1,2,4,null,3], to_delete = [3] Output: 1,2,4

---

Solutions

1. Pre-order Depth-First Search

Time Complexity: $O(n+m)$ | Space Complexity: $O(n+m)$, where n - number of nodes, m - number of values in to_delete

To solve this problem, we can iterate through the tree using DFS. In the solution below, I use pre-order traversal, although in-order or post-order traversals would also work. Whenever I encounter a node to delete, I access its parent and set the corresponding child to None. To determine which child to update, we pass is_left_child to each node with the correct value. To save the roots, we add them to a set roots.

class Solution:
    def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]:
 
        roots = set()
        roots.add(root)
 
        to_delete = set(to_delete)
 
        def dfs(parent, node, is_left_child):
            if not node:
                return
            
            if node.val in to_delete:
                to_delete.discard(node.val)
                roots.discard(node)
                if node.left: roots.add(node.left)
                if node.right: roots.add(node.right)
                if parent:
                    if is_left_child:
                        parent.left = None
                    else:
                        parent.right = None
 
            dfs(node, node.left, True)
            dfs(node, node.right, False)
 
        dfs(None, root, False)
 
        return list(roots)
 

---

2. Breadth-First Search

Time Complexity: $O(n+m)$ | Space Complexity: $O(n+m)$, where n - number of nodes, m - number of values in to_delete

A similar solution to the DFS approach above can be achieved using BFS.

class Solution:
    def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]:
 
        roots = set()
        roots.add(root)
 
        to_delete = set(to_delete)
        queue = deque([(None, root, False)])  # (parent, node, is_left_child)
 
        while queue:
            parent, node, is_left_child = queue.popleft()
 
            if node.val in to_delete:
                to_delete.discard(node.val)
                roots.discard(node)
                if node.left:
                    roots.add(node.left)
                if node.right:
                    roots.add(node.right)
                if parent:
                    if is_left_child:
                        parent.left = None
                    else:
                        parent.right = None
 
            if node.left:
                queue.append((node, node.left, True))
            if node.right:
                queue.append((node, node.right, False))
 
        return list(roots)
 

To showcase that there is not much difference between BFS and DFS implementations, I am attaching the screenshot below.