2058. Find the Minimum and Maximum Number of Nodes Between Critical Points

Problem

Question

A critical point in a linked list is defined as either a local maxima or a local minima. A node is a local maxima if the current node has a value strictly greater than the previous node and the next node. A node is a local minima if the current node has a value strictly smaller than the previous node and the next node. Note that a node can only be a local maxima/minima if there exists both a previous node and a next node. Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].

Example 1:

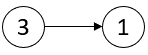
Input: head = [3,1] Output: [-1,-1] Explanation: There are no critical points in [3,1].

Example 2:

Input: head = [5,3,1,2,5,1,2] Output: [1,3] Explanation: There are three critical points:

• [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2.
• [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1.
• [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2. The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1. The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.

Example 3:

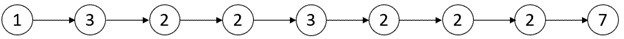
Input: head = [1,3,2,2,3,2,2,2,7] Output: [3,3] Explanation: There are two critical points:

• [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2.
• [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2. Both the minimum and maximum distances are between the second and the fifth node. Thus, minDistance and maxDistance is 5 - 2 = 3. Note that the last node is not considered a local maxima because it does not have a next node.

Constraints:

• The number of nodes in the list is in the range [2, 105].
• 1 <= Node.val <= 105

---

Solutions

Single Pass with Extra Space

Time Complexity: $O(n)$ | Space Complexity: $O(n)$

The solution involves identifying critical points, saving their indices in a separate array, and traversing through that array to find the minimum distance between consecutive critical points. The maximum distance is always the difference between the first and last indices.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def nodesBetweenCriticalPoints(self, head: Optional[ListNode]) -> List[int]:
 
        result = [-1, -1]
        critical_points = []
 
        i = 1
        prev = cur = head
        while cur.next.next:
            prev = cur
            cur = cur.next
            if prev.val < cur.val > cur.next.val:
                critical_points.append(i)
            if prev.val > cur.val < cur.next.val:
                critical_points.append(i)
            i += 1
        
        if len(critical_points) < 2:
            return result
 
        result[-1] = critical_points[-1] - critical_points[0]
        result[0] = float('inf')
        for i in range(len(critical_points) - 1):
            result[0] = min(result[0], critical_points[i + 1] - critical_points[i])
 
        return result
 

---

🏆 2. Single Pass, no Extra Space

Time Complexity: $O(n)$ | Space Complexity: $O(1)$

The approach above can be optimized further. To find the maximum distance, let’s save the first critical point in the variable first and the second critical point in last. We can also introduce a variable minimum to keep track of the smallest distance between consecutive critical points as we traverse the list.

If we find only 1 critical point, return [-1, -1].

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def nodesBetweenCriticalPoints(self, head: Optional[ListNode]) -> List[int]:
 
        def criticalPoint(prev, cur, next):
            return (prev.val < cur.val > cur.next.val) or (prev.val > cur.val < cur.next.val)
 
        minimum = float('inf')
        first = last = -1
 
        i = 1
        prev = cur = head
        while cur.next.next:
            prev = cur
            cur = cur.next
            if criticalPoint(prev, cur, cur.next):
                if first == -1: first = i
                if last != -1: minimum = min(minimum, i - last)
                last = i
            i += 1
        
        if last - first == 0:
            return [-1, -1]
 
        return [minimum, last - first]